The slope-intercept form‚ y = mx + b‚ is a fundamental equation in algebra for graphing lines. It simplifies identifying the slope (m) and y-intercept (b)‚ essential for understanding linear relationships and their real-world applications.
1.1 Definition and Importance
The slope-intercept form‚ y = mx + b‚ is a linear equation where m represents the slope and b is the y-intercept. This form is essential for graphing lines‚ as it directly provides the slope and the point where the line crosses the y-axis. Its simplicity makes it a foundational tool in algebra‚ enabling quick identification of key line characteristics. Understanding slope-intercept form is crucial for solving real-world problems involving linear relationships‚ such as calculating rates of change or predicting outcomes based on trends.
1.2 Brief History and Applications
The slope-intercept form‚ y = mx + b‚ has its roots in ancient mathematics‚ evolving from linear equation studies. It became a cornerstone in algebra for its simplicity in graphing and analyzing linear relationships. Widely applied in physics‚ economics‚ and engineering‚ it aids in modeling real-world phenomena‚ such as motion and financial trends. Its practical applications make it an essential tool for problem-solving and predictive analysis in various scientific and real-world contexts.

Key Components of Slope-Intercept Form
The slope-intercept form consists of two main components: the slope (m) and the y-intercept (b). The slope indicates the steepness of the line‚ while the y-intercept is the point where the line crosses the y-axis. Together‚ they define the equation y = mx + b‚ making it easy to graph and analyze linear relationships.
2.1 Understanding Slope (m)
The slope (m) represents the steepness of a line‚ calculated as the change in y over the change in x. It can be positive‚ negative‚ or zero‚ indicating an upward‚ downward‚ or flat line‚ respectively. A steeper slope means a larger absolute value of m. For example‚ a slope of 2 increases by 2 units for every 1 unit moved to the right‚ while a slope of -1 decreases by 1 unit for every 1 unit moved to the right. Understanding slope is crucial for graphing and interpreting linear equations‚ as it provides immediate visual information about the line’s direction and steepness. Worksheets often include exercises where students identify slope from equations or graphs‚ ensuring mastery of this concept‚ which is foundational for more complex algebraic topics. Additionally‚ real-world applications‚ such as calculating inclines or rates of change‚ rely heavily on accurately determining slope‚ making it a vital skill in various fields beyond mathematics‚ including physics and engineering. By practicing with slope-intercept form worksheets‚ students can solidify their understanding of slope and its practical implications.
2.2 Understanding Y-Intercept (b)
The y-intercept (b) is the point where the line crosses the y-axis. It is a constant value in the slope-intercept form equation y = mx + b. The y-intercept provides essential information for graphing lines‚ as it identifies the starting point of the line on the y-axis. For example‚ in the equation y = 2x + 3‚ the y-intercept is 3‚ meaning the line crosses the y-axis at (0‚ 3). Worksheets often include exercises where students identify the y-intercept from equations or graphs‚ helping them understand its role in defining the line’s position. A positive y-intercept indicates the line starts above the origin‚ while a negative y-intercept indicates it starts below. Accurately identifying the y-intercept is crucial for correctly graphing and interpreting linear equations‚ making it a fundamental concept in algebra and its applications. Practice with slope-intercept form worksheets ensures students grasp this key component effectively‚ enhancing their ability to analyze and visualize linear relationships. The y-intercept‚ along with the slope‚ forms the backbone of understanding linear equations in various real-world contexts‚ from finance to science. By mastering the y-intercept‚ students can better comprehend how lines behave and interact within coordinate systems‚ preparing them for more advanced mathematical studies. The combination of slope and y-intercept allows for precise descriptions of linear relationships‚ making them indispensable tools in data analysis and modeling. Through consistent practice and exposure to diverse problems‚ students develop a robust understanding of the y-intercept’s significance in slope-intercept form‚ enabling them to apply this knowledge across different mathematical and practical scenarios. The y-intercept’s role in defining a line’s position complements the slope’s role in determining its direction‚ together providing a complete description of a linear equation’s graph. This dual understanding is essential for solving real-world problems that involve linear relationships‚ such as calculating distances‚ predicting trends‚ and optimizing processes. By focusing on the y-intercept in worksheets and exercises‚ educators help students build a strong foundation in linear algebra‚ which is critical for advancing in mathematics and related fields. The y-intercept serves as a cornerstone in the study of linear equations‚ offering insights into how lines are structured and how they can be manipulated to solve various problems. As students progress‚ the concepts learned from the y-intercept will be applied to more complex mathematical ideas‚ emphasizing the importance of a solid understanding at this stage. The integration of y-intercept and slope in the slope-intercept form equation y = mx + b creates a powerful tool for analyzing and graphing lines‚ making it an essential part of any algebra curriculum. By engaging with slope-intercept form worksheets‚ students not only improve their technical skills but also develop problem-solving abilities that are valuable in numerous academic and professional settings. The y-intercept’s clear and direct interpretation makes it an accessible yet profound concept‚ bridging the gap between theoretical mathematics and practical application. This accessibility allows students to grasp the fundamentals of linear equations without becoming overwhelmed‚ providing a smooth transition into more challenging topics. In conclusion‚ the y-intercept is a vital component of the slope-intercept form‚ offering students a clear and tangible way to understand how lines are positioned and behave within a coordinate system. Through dedicated practice and exposure to various problems‚ students can master the concept of the y-intercept‚ equipping themselves with the skills necessary to excel in algebra and beyond.
2.3 Examples of Slope and Y-Intercept
Examples help clarify the concepts of slope (m) and y-intercept (b). For instance‚ in the equation y = 2x + 3‚ the slope is 2‚ indicating a steepness of 2 units up for every 1 unit right‚ and the y-intercept is 3‚ crossing the y-axis at (0‚ 3). Another example‚ y = -4x ー 5‚ has a slope of -4 (declining) and a y-intercept of -5‚ crossing the y-axis at (0‚ -5). These examples demonstrate how slope and y-intercept define a line’s behavior and position. Worksheets often include such examples to help students practice identifying and interpreting these components‚ reinforcing their understanding of linear equations.

Converting Standard Form to Slope-Intercept Form
To convert standard form (Ax + By = C) to slope-intercept form (y = mx + b)‚ isolate y by subtracting Ax and dividing by B. For example‚ 4x ⸺ 2y = 12 becomes y = -2x + 6. This process helps in identifying the slope and y-intercept easily. Worksheets often include such exercises to practice this fundamental skill.
3.1 Step-by-Step Conversion Process
To convert standard form (Ax + By = C) to slope-intercept form (y = mx + b)‚ follow these steps:
- Subtract the Ax term from both sides to isolate the y-term: By = -Ax + C.
- Divide every term by B to solve for y: y = (-A/B)x + (C/B).
- Simplify the equation to identify the slope (m = -A/B) and y-intercept (b = C/B).
For example‚ converting 4x + 2y = 8:
- 2y = -4x + 8
- y = -2x + 4
This process ensures the equation is in slope-intercept form‚ making it easier to graph and analyze linear relationships. Worksheets often include practice exercises to master this conversion.
3.2 Example Problems and Solutions
Convert the following standard form equations to slope-intercept form:
- Problem 1: 4x + 2y = 8
- Solution: 2y = -4x + 8 → y = -2x + 4
- Problem 2: 3x ⸺ 4y = 12
- Solution: -4y = -3x + 12 → y = (3/4)x ⸺ 3
- Problem 3: 2x + 5y = 15
- Solution: 5y = -2x + 15 → y = (-2/5)x + 3
These examples demonstrate how to isolate y and identify the slope (m) and y-intercept (b). Worksheets often include similar exercises to practice this skill.

Graphing Lines in Slope-Intercept Form
Graphing lines in slope-intercept form involves plotting the y-intercept and using the slope to find additional points. Start at (0‚ b)‚ then move m units up/down for each unit right/left. Ensure accuracy by checking multiple points.
4.1 Plotting the Y-Intercept
Plotting the y-intercept is the first step in graphing a line in slope-intercept form. Identify the y-intercept (b) from the equation y = mx + b. Locate the point (0‚ b) on the y-axis and mark it. This point is where the line crosses the y-axis. Use this starting point to plot additional points using the slope (m). For example‚ in y = 2x + 3‚ the y-intercept is (0‚ 3). Plot this point and use the slope to continue drawing the line accurately.
4.2 Using Slope to Plot Additional Points
After plotting the y-intercept‚ use the slope (m) to determine additional points on the line. The slope represents the rise over run‚ indicating how many units to move up or down for every unit moved to the right or left. For example‚ a slope of 2 means moving 2 units up for every 1 unit right. Start from the y-intercept and apply the slope to plot several points‚ ensuring the line is drawn accurately and consistently. This step helps in visualizing the line’s direction and steepness.
4.3 Tips for Accurate Graphing
For precise graphing‚ start by accurately plotting the y-intercept and using the slope to determine additional points. Ensure the line is drawn straight using a ruler; Double-check calculations to avoid errors. Label axes clearly and use consistent scales. Verify each plotted point aligns with the slope. For negative slopes‚ move left/down instead of right/up. Use reference points to maintain consistency. If unsure‚ plot multiple points and draw the line carefully. This ensures an accurate representation of the equation.
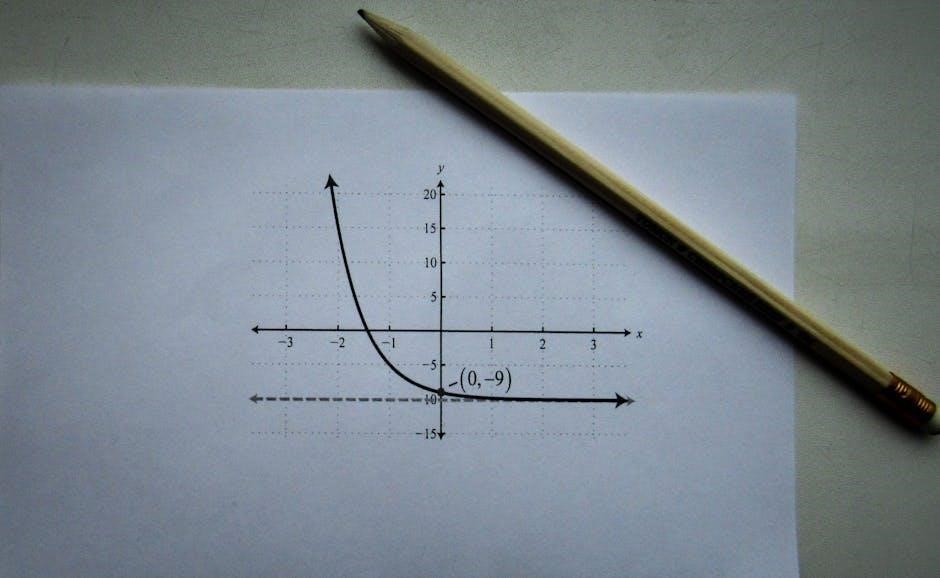
Identifying Slope and Y-Intercept from a Graph
Identify the y-intercept where the line crosses the y-axis. Calculate the slope by dividing the change in y by the change in x between two points on the line. Use clear examples to ensure accuracy.
5.1 Locating the Y-Intercept on a Graph
To locate the y-intercept on a graph‚ find where the line crosses the y-axis. This point is always in the form (0‚ b)‚ where b is the y-intercept. Ensure the line is clearly visible and accurately identify the value of b by reading the scale on the y-axis. This step is crucial for determining the equation of the line in slope-intercept form‚ y = mx + b.
5.2 Calculating Slope from a Graph
To calculate the slope from a graph‚ identify two distinct points (x1‚ y1) and (x2‚ y2) that the line passes through. Use the formula: slope (m) = (y2 ー y1) / (x2 ー x1). Ensure the points are clear and easy to read. Measure the vertical change (rise) and horizontal change (run) between the points. If the line rises from left to right‚ the slope is positive; if it falls‚ the slope is negative. A horizontal line has a slope of 0. Calculate carefully to avoid errors.
5.3 Practice Exercises
- Identify the slope and y-intercept for each line graphed on the provided worksheet.
- Convert standard form equations to slope-intercept form and identify key components.
- Calculate the slope between given points using the rise-over-run formula.
- Plot lines on a graph using the slope and y-intercept from the equation.
- Solve word problems by writing equations in slope-intercept form.
These exercises reinforce understanding and application of slope-intercept form concepts through practical application and problem-solving.

Writing Equations in Slope-Intercept Form
Learn to write equations in slope-intercept form (y = mx + b) using given slopes‚ y-intercepts‚ or points. Practice converting standard form equations to slope-intercept form for better understanding and application.
6.1 Given Slope and Y-Intercept
When provided with the slope (m) and y-intercept (b)‚ writing the equation in slope-intercept form is straightforward. Simply substitute the given values into the equation y = mx + b. For example‚ if the slope is 2 and the y-intercept is 3‚ the equation becomes y = 2x + 3. This method ensures clarity and accuracy in representing linear relationships. Practice worksheets are available to refine this skill.
6.2 From a Graph
To write the equation of a line in slope-intercept form from a graph‚ identify the y-intercept (b) where the line crosses the y-axis. Next‚ calculate the slope (m) by selecting two points on the line and applying the formula ( m = rac{y_2 ー y_1}{x_2 ー x_1} ). Substitute these values into the equation ( y = mx + b ). Practice worksheets and online tools can help refine this process for accuracy and speed.
6.3 Through Two Points
To write the equation of a line in slope-intercept form through two points‚ first calculate the slope (m) using the formula ( m = rac{y_2 ー y_1}{x_2 ⸺ x_1} ). Once the slope is determined‚ substitute the slope and one of the points into the equation ( y = mx + b ) to solve for the y-intercept (b). Practice worksheets and online tools are available to help master this method‚ ensuring accuracy in deriving the equation from given points.
Common Errors and Misconceptions
Common errors include misidentifying slope and y-intercept‚ handling negative values incorrectly‚ and calculation mistakes. Practice with worksheets helps avoid these issues and ensures accurate equation writing.
7.1 Misidentifying Slope and Y-Intercept
A common error is confusing the slope (m) and y-intercept (b) in the equation y = mx + b. Students often mistakenly identify the y-intercept as the slope or vice versa. This misunderstanding can lead to incorrect graphing and equation writing. Negative slopes and intercepts further complicate identification‚ as students may overlook the negative sign. Worksheets and practice exercises emphasize clear identification and proper labeling to avoid such mistakes and ensure accuracy in linear equations.
7.2 Handling Negative Slopes and Intercepts
Negative slopes and y-intercepts can be challenging for students‚ often leading to errors in graphing and equation interpretation. A negative slope indicates a decreasing line‚ while a negative y-intercept means the line crosses the y-axis below the origin. Worksheets often include practice problems with negative values to help students recognize and correctly plot these scenarios‚ reinforcing the importance of attentiveness to signs and their impact on the line’s direction and position.
7.3 Avoiding Calculation Mistakes
Calculation mistakes are common when converting equations to slope-intercept form or identifying components. Errors often occur when isolating y or misidentifying m and b. Pay close attention to signs‚ especially with negative slopes or intercepts. Double-check arithmetic and ensure the equation is fully simplified. Practicing with worksheets and using online tools can help build accuracy and confidence in handling slope-intercept form calculations effectively.



